Would you rather win the argument and make the right call. We need to make an unbiased judgment.
This short book aims to help us avoid common stats mistakes in daily life. But, unfortunately, it happens too often and can ruin our ability to act right!
Action: Use a REAL random sample and consider proportion.
3 Key Concepts
- Is this sample really random? Does it truly represent the real data?
- Is there a correlation between the model’s X variable and the error term?
- Bayes’ Theorem: proportion vs. probability to quantify belief
Thinking Statistically is a Traning
In daily conversation, we tend to make extreme statements. This is also my biggest guilt during the debate. We throw extraordinary facts at each other to prove our point that something is justified. Of course, these arguments are, in many cases, merely an exception. But both speakers and audiences like to hear them. For example, we want to talk about extremely successful figures in each field, superstars, geniuses, etc.
Be aware! These outliers are also an "extremely bad" sample.
Endogeneity: X(a) = Y(b) + Z; a=kb. X and Y are dependent.
At first, you do not see it. However, without being aware of the dependency, you might eliminate the factor that leads to a solution or misinterpret the meaning of the model.
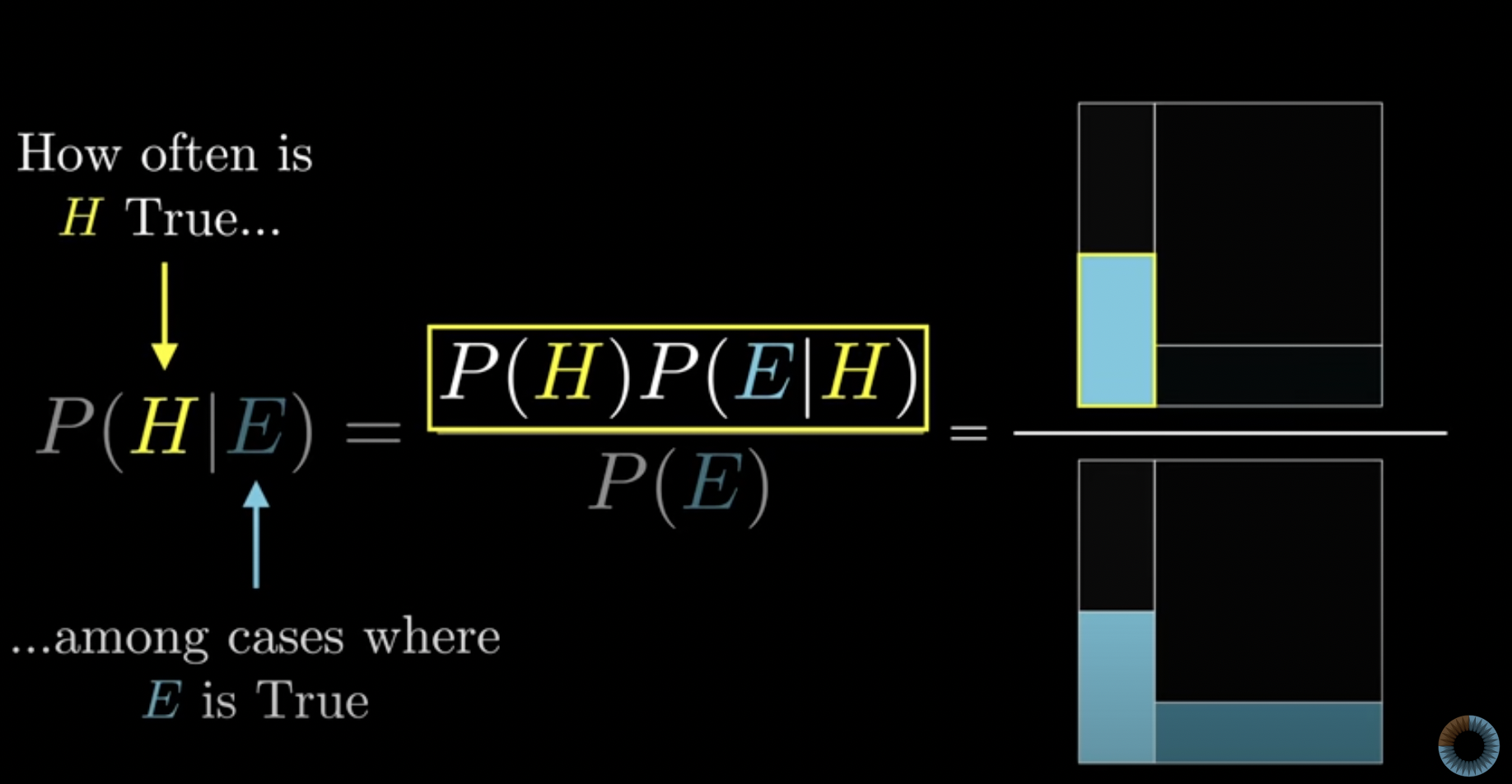
Bayes’ Theorem: “Perhaps the most important formula in probability.”
Check out this video from 3Blue1Brown. The probability shows how often an event (H) is true among cases where cases (E) are true. This Theorem helps one to understand both in terms of ratio and proportion of the occurrence.
For example, the probability that a quiet and book-loving person would be a librarian compared to a farmer. One might think that the description fits a librarian better than a farmer. But when we consider how few librarians and how many farmers there are in a population, one would see that there is a bigger chance that such a person is a farmer rather than a librarian.
Today, we have learned common statistics mistakes when choosing a sample to give as an example, a dependent model, and the probability of proportion.
Get this book on Amazon here!

